Notes

Topology and Topological Spaces: A Primer

The study of topological spaces is a generalisation of the concepts of metric spaces, as well as open and closed sets, both of which are important in real analysis. Informally, a topological space is a set that has a topology, which "decides" which subset is open or not.

Definition. A topology $\mathcal{T}$ on a set $X$ is a collection of subsets of $X$ (in other words, $\mathcal{T} \subseteq \mathcal{P}(X)$) which has the following properties:

1. The empty set $\emptyset$ and $X$ itself are in $\mathcal{T}$.
2. Any arbitrary union of subcollections of $\mathcal{T}$ is in $\mathcal{T}$.
3. Any finite intersection of subcollections of $\mathcal{T}$ is in $\mathcal{T}$.

We can then say that a subset $U$ of $X$ is an open set if $X$ is in $\mathcal{T}$. One can compare this with the metric-space definition of open sets, which is the definition often adapted in real analysis courses and can allow us to derive the topological definition of open sets in $X$, as described above.

One may then ask: what if it is the other way round, i.e. is it possible to produce a metric space from a topological space? In fact, this is a question that attracts so much interest that mathematicians assign a special name to those that have this property: metrizable spaces, which we shall learn later in this chapter.

This may look obvious to some, but for the sake of reminder: it is possible for a set $X$ to have multiple topologies. There is also a not-so-obvious one: different sets can have the same topology(!).

Concepts for Topologies

Fineness and Coarseness

Definition. Given (any) two topologies $\mathcal{T}, \mathcal{T'}$ of a set $X$, we say that $\mathcal{T'}$ is finer than $\mathcal{T}$ if $\boxed{\mathcal{T'} \supseteq \mathcal{T}}$. We say $\mathcal{T'}$ is strictly finer than $\mathcal{T}$ if $\boxed{\mathcal{T'} \supset \mathcal{T}}$.

Conversely, if $\boxed{\mathcal{T'} \subseteq \mathcal{T}}$ (resp. $\boxed{\mathcal{T'} \subset \mathcal{T}}$), then we say that $\mathcal{T'}$ is coarser (resp. strictly coarser) than $\mathcal{T}$.

We say $\mathcal{T}$ and $\mathcal{T'}$ are comparable if either $\mathcal{T'} \supseteq \mathcal{T}$ or $\mathcal{T'} \subseteq \mathcal{T}$, i.e. if it is possible to say if one is finer or coarser than the other.

Informally, a topology is finer if it "contains more detail" or "has a finer scale" than the other topology.

A visualisation of topological coarseness and fineness using ruler markings.

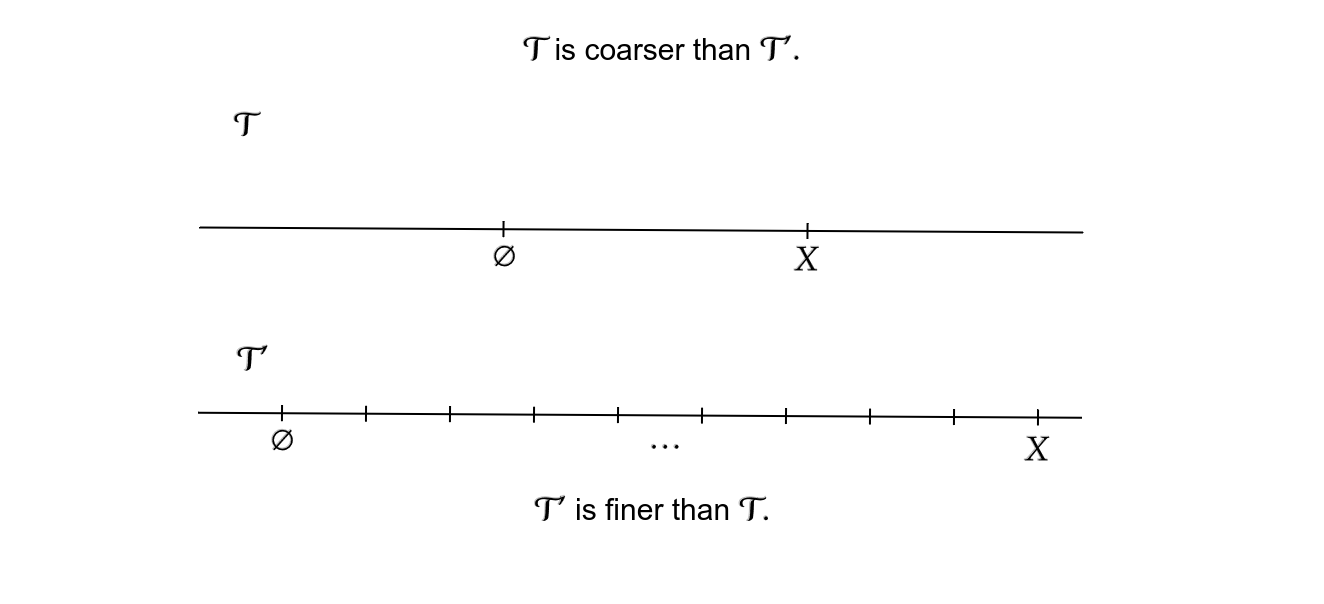
Note that if $\mathcal{T}$ and $\mathcal{T}'$ are coarser/finer than each other, then they are the same topology.

Basis (for a Topology)

Basic building blocks of a topology.

Definition. Let $X$ be a set. A basis for a topology $\mathcal{T}$ on $X$ is a collection of subsets of $X$ (which are called basis elements), denoted here as $\mathcal{B}$, such that for each $x \in X$:-

1. There is at least one basis element $B$ that contains $x$, i.e. $x \in B$.
2. If $x \in B_1 \cap B_2$, where $B_1$ and $B_2$ are (two) basis elements, then there is a (third) basis element $B_3$ such that $x \in B_3$ and $B_3$ is contained by the intersection of $B_1$ and $B_2$, i.e. $B_3 \subseteq B_1 \cap B_2$. (Note: this is immediately true if $B_1 = B_2$: the desired $B_3$ will just be $B_1 = B_2$ itself.)

The topology $\mathcal{T}$ generated by the basis $\mathcal{B}$ is then defined as: if a subset $U$ of $X$ is open (i.e. $U \in \mathcal{T}$), then for each $x \in U$, there is a basis element $B \in \mathcal{B}$ such that $x \in B$ and $B \subseteq U$. From the definition, we can see that the basis elements themselves are in the topology generated from them.

Why does this definition of basis-generated topology do give us a topology?

We need to check that a topology $\mathcal{T}$ generated by a basis $\mathcal{B}$ satisfies the basic definition of topology.

If $U = \emptyset$, then $U \in \mathcal{T}$ vacuously because we cannot find any $x \in U$ to check the condition of openness. If $U = X$, then since every basis element $B \in \mathcal{B}$ satisfies $B \subseteq X$, as well as the first condition for a basis, it also satisfies this condition of openness and is thus in $\mathcal{T}$.

To check that any arbitrary union of $\mathcal{T}$, i.e. $U = \bigcup_{\alpha \in J}U_\alpha$, where $\{U_\alpha\}_{\alpha \in J}$ is an indexed family of sets in $\mathcal{T}$, is still in $\mathcal{T}$, we see that since each $U_\alpha$ is open, by definition, there is a basis element $B$ such that $x \in B \subseteq U_\alpha$. Note that $U_\alpha \subseteq U$ for any $\alpha \in J$, so we have $B \subseteq U$ as well. This shows that $U$ is open and hence in $\mathcal{T}$.

To check that any finite intersection of $\mathcal{T}$, i.e. $U = \bigcap_{i=1}^{n}U_i$, where $U_1,\ldots, U_n \in \mathcal{T}$ and $n \in \mathbb{N}$, is in $\mathcal{T}$, we can do so by induction. We first settle the base case: for $n = 1$, $U_1$ itself is already in $\mathcal{T}$, so it immediately holds.

When $n = 2$ so that we have $U_1 \cap U_2$, given $x \in U_1 \cap U_2$, by definition, we can choose basis elements $B_1$ and $B_2$ such that $x \in B_1$ (resp. $B_2$) and $B_1 \subseteq U_1$ (resp. $B_2 \subseteq U_2$). By the definition of a basis, we can obtain a basis element $B_3$ such that $x \in B_3$ and $B_3 \subseteq B_1 \cap B_2$. Since $B_1 \cap B_2 \subseteq U_1 \cap U_2$, this gives us $B_3 \subseteq U_1 \cap U_2$, so $U_1 \cap U_2 \in \mathcal{T}$, by definition.

This argument above can be used to prove the inductive case. For a finite intersection $U_1 \cap \cdots \cap U_n$ of elements of $\mathcal{T}$, we first suppose that $U_1 \cap \cdots \cap U_{n-1}$ does belong to $\mathcal{T}$. Now, note that

$$(U_1 \cap \cdots \cap U_n) = (U_1 \cap \cdots \cap U_{n-1}) \cap U_n.$$

Therefore, by induction hypothesis and applying the argument above, we can conclude that any finite intersection of elements in $\mathcal{T}$ belongs to $\mathcal{T}$.

We have then checked that all three conditions of a topology are satisifed, so $\mathcal{T}$ indeed gives us a topology.

If $X$ is any set, the collection of all one-point subsets (singletons) of $X$ is a basis for the discrete topology on $X$. Why?

Let $X$ be a set and $\mathcal{B}$ be the collection of all one-point subsets of $X$. Since there is a one-to-one correspondence, specifically $x \mapsto \{x\}$, between $X$ and $\mathcal{B}$, this allows us to conclude that for any $x \in X$, there exists at least one basis element $B \in \mathcal{B}$ such that $x \in B$, giving us the first condition for a basis. Due to this one-to-one correspondence as well, there is no elements in $X$ that belongs to two different basis elements, so the second condition for a basis holds vacuously.

Any arbitrary union of the one-point subsets $B \in \mathcal{B}$ will give us $\mathcal{P}(X) \backslash \{\emptyset\}$, i.e. the collection of all subsets of $X$ except for the empty set, and this indeed includes $X$ itself. Any finite intersection of $B$ will then give us the last piece of the puzzle: the empty set $\emptyset$.

This finally gives us the complete $\mathcal{P}(X)$, i.e. the discrete topology on $X$.

[Lemma 13.1] $\mathcal{T}$ as a topology on a set $X$ that is generated by a basis $\mathcal{B}$ can also be described as the collection of all unions of elements of $\mathcal{B}$. Why?

For any given collection of elements of $\mathcal{B}$, since they are also elements of $\mathcal{T}$ and $\mathcal{T}$ is a topology, their union is also in $\mathcal{T}$.

Conversely, for any $U \in \mathcal{T}$, we can find for each $x \in U$ a basis element $B_x \in \mathcal{B}$ such that $x \in B_x \subseteq U$, so $U = \bigcup_{x \in U}B_x$, and thus $U$ equals a union of elements of $\mathcal{B}$.

warning

This means that any open set $U$ in $X$ can be expressed a union of basis elements, which sounds analogous to bases in linear algebra in which vectors are expressed as a linear combination of basis vectors. However, such expression needs not be unique, which makes it different from bases in linear algebra, which are unique.

In reverse, we can also obtain a basis for a given topology, which is a frequently cited fact in the study of this topic.

[Lemma 13.2] Let $X$ be a topological space. Suppose that $\mathcal{C}$ is a collection of open sets of $X$ such that for each open set $U$ of $X$ and each $x$ in $U$, there is an element $C$ of $\mathcal{C}$ such that $x \in C \subseteq U$, then $\mathcal{C}$ is a basis for the topology of $X$. Why?

We need to check that $\mathcal{C}$ satisifies the defining conditions of a (topological) basis. Since $X$ is a topological space and thus is an open set itself, by the hypothesis for $\mathcal{C}$, for each $x \in U$, there is an element $C$ of $\mathcal{C}$ such that $x \in C \subseteq X$, so the first condition is satisfied.

To check the second condition, suppose that $x \in C_1 \cap C_2$, where $C_1,C_2 \in \mathcal{C}$. Since $C_1$ and $C_2$ are open, so is $C_1 \cap C_2$. Therefore, there exists by hypothesis an element $C_3$ in $\mathcal{C}$ such that $x \in C_3 \subseteq C_1 \cap C_2$.

Let $\mathcal{T}$ be the collection of open sets of $X$; we also need to show that the topology $\mathcal{T}'$ generated by $\mathcal{C}$ is indeed equal to the topology $\mathcal{T}$. First, note that if $U$ belongs to $\mathcal{T}$ and if $x \in U$, then there is by hypothesis an element $C$ of $\mathcal{C}$ such that $x \in C \subseteq U$, so $U$ belongs to the (generated) topology $\mathcal{T}'$. Conversely, if $W$ belongs to the (generated) topology $\mathcal{T}'$, then $W$ equals a union of elements of $\mathcal{C}$, by Lemma 13.1. Since each element of $\mathcal{C}$ belongs to $\mathcal{T}$ and $\mathcal{T}$ is a topology, $W$ also belongs to $\mathcal{T}$.

[Lemma 13.3] Let $\mathcal{B}$ and $\mathcal{B}'$ be bases for the topologies $\mathcal{T}$ and $\mathcal{T}'$, respectively, on $X$, then $\mathcal{T}'$ is finer than $\mathcal{T}$ if and only if for each $x \in X$ and each basis element $B \in \mathcal{B}$ containing $x$, there is a basis element $B' \in \mathcal{B}'$ such that $x \in B' \subseteq B$.

Proof of Lemma 13.3.

$(\impliedby)$. Given an element $U$ of $\mathcal{T}$, we wish to show that $U \in \mathcal{T}'$. Let $x \in U$. Since $\mathcal{B}$ generates $\mathcal{T}$, there is an element $B \in \mathcal{B}$ such that $x \in B \subseteq U$. By hypothesis, there exists an element $B' \in \mathcal{B}'$ such that $x \in B' \subseteq B$, then $x \in B' \subseteq U$, so $U \in \mathcal{T}'$ by definition.

$(\implies)$. Let $x \in X$ and $B \in \mathcal{B}$, with $x \in B$. Now $B$ belongs to $\mathcal{T}$ by definition and $\mathcal{T} \subseteq \mathcal{T}'$ by hypothesis (being finer). Therefore, $B \in \mathcal{T}'$. Since $\mathcal{T}'$ is generated by $\mathcal{B}'$, there is an element $B' \in \mathcal{B}'$ such that $x \in B' \subseteq B$.

note

Using Lemma 13.3, we can see that the collection of all circular regions in the plane generates the same topology as the collection of all rectangular regions.

Definition. A subbasis $\mathcal{S}$ for a topology on $X$ is a collection of subsets of $X$ whose union equals $X$. The topology generated by the subbasis $\mathcal{S}$ is defined to be the collection $\mathcal{T}$ of all (arbitrary) unions of finite intersections of elements of $\mathcal{S}$.

Sanity check of the definition of subbasis-generated topology.

It suffices to show that the collection $\mathcal{B}$ of all finite intersections of elements of $\mathcal{S}$ is a basis for $\mathcal{T}$, as we can then apply Lemma 13.1 to conclude that the collection $\mathcal{T}$ of all unions of elements of $\mathcal{B}$ is indeed a topology as desired.

Given $x \in X$, it belongs to an element of $\mathcal{S}$ by definition of subbasis, so it also belongs to an element of $\mathcal{B}$; this shows the first condition for a basis. To check the second condition (that involves intersection), consider the following two elements of $\mathcal{B}$,

$$B_1 := S_1 \cap \cdots \cap S_m \quad \text{and} \quad B_2 := S_1' \cap \cdots \cap S_n'.$$

Their intersection

$$B_1 \cap B_2 = (S_1 \cap \cdots \cap S_m) \cap (S_1' \cap \cdots \cap S_n')$$

is also a finite intersection of elements of $\mathcal{S}$, so it belongs to $\mathcal{B}$.

note

Munkres' definition of subbasis here is different from that given in the corresponding Wikipedia article. In Wikipedia's definition, the topology generation is considered given, rather than a consequence.

It is also worth noting that in Rudin's Functional Analysis, a subbasis is defined to be a subcollection $B$ of an established topology such that the collection of open sets consisting of all finite intersections of elements of $B$ forms a basis for the topology. This is something that requires proof in Munkres, but is taken for granted in Rudin.

tip

Don't think of the use of the prefix 'sub' in the word 'subbasis' here in the same way as the way as 'subset' does, but more like the word 'subpar': it doesn't mean that it is contained by a larger (topological) basis as a collection of basis elements; instead, think of it as 'something that is not quite a basis yet but serves a foundation to it.'

Important Topologies

There are several main topologies covered in this chapter. Some of them are so important that they deserve a dedicated subsection, whereas some others that are not so much are just included as an item of a bullet list here. Here, we denote a set as $X$, and its equipped topology, unless otherwise stated, as $\mathcal{T}$.

• Discrete topology: the collection of all subsets of $X$.
• Indiscrete/trivial topology: the other end of the extreme, i.e. the collection of only $\emptyset$ and $X$ itself.
• Finite complement topology (a.k.a. cofinite topology), $\mathcal{T}_f$: the collection of all subsets $U$ of $X$ such that $X \backslash U$ is either finite or $X$ itself (so that $U = \emptyset$).
• Countable complement topology, $\mathcal{T}_c$: the collection of all subsets $U$ of $X$ such that $X \backslash U$ is either countable or $X$ itself (so that $U = \emptyset$).
• Standard topology (on the real line), $\mathbb{R}$: the topology generated by the collection of all open intervals in the real line, $(a,b)=\{x : a < x < b\}$. This is assumed to be the default topology for $\mathbb{R}$, unless otherwise stated.
• Lower limit topology, $\mathbb{R}_l$: the topology generated by the collection of all half-open intervals of the form $[a,b) = \{x : a \leqslant x < b\}$, where $a < b$.
• K-topology, $\mathbb{R}_K$: the topology generated by the collection of all open intervals $(a,b)$, along with all sets of the form $(a,b) \backslash K$, where $K = \left\{\frac{1}{n} : n \in \mathbb{Z}_+ \right\}$.

[Lemma 13.4] The topologies of $\mathbb{R}_l$ and $\mathbb{R}_K$ are strictly finer than the standard topology on $\mathbb{R}$, but are not comparable with one another.

Proof of Lemma 13.4.

Let $\mathcal{T}$, $\mathcal{T}'$ and $\mathcal{T}''$ be the standard $\mathbb{R}$-topology, lower limit topology and K-topology respectively. Lemma 13.3 will be applied in the proof here.

Given a basis element $(a,b)$ for $\mathcal{T}$ and a point $x$ inside $(a,b)$, the basis element $[x,b)$ for $\mathcal{T}'$ contains $x$ and lies in $(a,b)$. On the other hand, given the basis element $[x,d)$ for $\mathcal{T}'$, there is no open interval $(a,b)$ that contains $x$ and lies in $[x,d)$. Thus $\mathcal{T}'$ is strictly finer than $\mathcal{T}$.

Similarly, given a basis element $(a,b)$ for $\mathcal{T}$ and a point $x$ of $(a,b)$, this same interval is a basis element for $\mathcal{T}''$ that contains $x$. On the other hand, consider the basis element $B = (-1,1) \backslash K$ for $\mathcal{T}''$ and the point $0$ of $\mathcal{B}$, there is no open interval that contains $0$ and lies in $B$ (any open interval that contains $0$ must contain $\frac{1}{n}$ for some $n \in \mathbb{Z}_+$). Thus, $\mathcal{T}''$ is strictly finer than $\mathcal{T}$.

The proof for the non-comparability between $\mathbb{R}_l$ and $\mathbb{R}_K$ is a solution to Exercise 13.6.

Order Topology

An order topology is the generalisation of the topologies on $\mathbb{R}$ that are generated by intervals to any set with a simple order (a.k.a. strict total order).

Definition. Let $X$ be a set with a simple order relation and assume that $X$ has more than one element. Let $\mathcal{B}$ be the collection of all sets of the following types:

1. All open intervals $(a,b)$ in $X$.
2. All intervals of the form $[a_0,b)$, where $a_0$ is the smallest element (if any) of $X$.
3. All intervals of the form $(a,b_0]$, where $b_0$ is the largest element (if any) of $X$.

The collection $\mathcal{B}$ is then a basis for a topology on $X$, which is called the order topology.

note

If $X$ has no smallest element, there are no sets of the second type. If $X$ has no largest element, there are no sets of the third type.

Check that the collection $\mathcal{B}$ is a basis.

1. Indeed, every element $x$ of $X$ lies in at least one element of $\mathcal{B}$: the smallest element (if any) is in all sets of the second type, the largest element (if any) is in all sets of the third type and every other element is in a set of the first type.

2. The intersection of any two sets of the preceding types is again a set of one of these types, or is empty (if the two sets are disjoint).

   Assuming the two sets are not disjoint,

   • the intersection of two open intervals $(a,b)$ and $(a',b')$ is $(\max\{a,a'\}, \min\{b,b'\})$, an open interval;
   • the intersection of two intervals $(a,b)$ and $[a_0, b')$ is $(a,\min\{b,b'\})$;
   • the intersection of two intervals $(a,b)$ and $(a',b_0]$ is $(\max\{a,a'\},b)$;
   • the intersection of two intervals $[a_0,b)$ and $(a,b_0]$ is $(a,b)$.
   • the intersection of two intervals $[a_0,b)$ and $[a_0,b')$ is $[a_0,\min\{b,b'\})$;
   • the intersection of two intervals $(a,b_0]$ and $(a',b_0]$ is $(\max\{a,a'\}, b_0]$.

Definition. If $X$ is an ordered set, and $a$ is an element of $X$, there are four subsets of $X$ that are called rays determined by $a$. They are the following:

$$(a,+\infty) = \{x : x > a\}$$ $$(-\infty,a) = \{x : x < a\}$$ $$[a,+\infty) = \{x : x \geqslant a\}$$ $$(-\infty,a] = \{x : x \leqslant a\}$$

Sets of the first two types are called open rays, and sets of the last two types are called closed rays.

:::

Subspace Topology (a.k.a. Induced Topology)¹

Definition. Let $X$ be a topological space with a topology $\mathcal{T}$. If $Y$ is a subset of $X$, then the collection

$$\mathcal{T}_Y = \{ Y \cap U : U \in \mathcal{T} \}$$

which are all intersections of open sets of $X$ with $Y$, is a topology on $Y$, and we call it the subspace topology. With this topology, $Y$ is called a subspace of $X$.

[Lemma 16.1] If $\mathcal{B}$ is a basis for the topology of $X$ then the collection

$$\mathcal{B}_Y = \{B \cap Y : B \in \mathcal{B}\}$$

is a basis for the subspace topology on $Y$.

[Lemma 16.2] Let $Y$ be a subspace of $X$. If $U$ is open in $Y$ and $Y$ is open in $X$, then $U$ is open in $X$.

[Theorem 16.3] If $A$ is a subspace of $X$ and $B$ is a subspace of $Y$, then the product topology on $A \times B$ is the same as the topology $A \times B$ inherits as a subspace of $X \times Y$.

Given an ordered set $X$, let us say that a subset $Y$ of $X$ is convex in $X$ if for each pair of points $a < b$ of $Y$, the entire interval $(a,b)$ of points of $X$ lies in $Y$.

(Note that this implies that intervals and rays in $X$ are convex in $X$.)

[Theorem 16.4] Let $X$ be an ordered set in the order topology; let $Y$ be a subset of $X$ that is convex in $X$. Then the order topology on $Y$ is the same as the topology $Y$ inherits as a subspace of $X$.

warning

Note that without the restriction that $Y$ needs to be convex in $X$, Theorem 16.4 is not true in general.

A counterexample is given as follows: let $I = [0,1]$. The dictionary order on $I \times I$ is just the restriction to $I \times I$ of the dictionary order on the plane $\mathbb{R} \times \mathbb{R}$. However, the dictionary order topology on $I \times I$ is NOT the same as the subspace topology on $I \times I$ obtained from the dictionary topology on $\mathbb{R} \times \mathbb{R}$! For example, the set $U := \left\{\frac{1}{2}\right\} \times \left(\frac{1}{2}, 1\right]$ is open in $I \times I$ in the subspace topology, as it is the intersection of $I \times I$ with $V := \left(\left(\frac{1}{2},\frac{1}{2}\right), \left(\frac{1}{2}, 50\right)\right)$ and $V$ is open in $\mathbb{R} \times \mathbb{R}$, but $U$ is not open in the order topology, as any basis element for the order topology on $I \times I$ that contains $U$ must contain points of $I \times I$ such that the first coordinate is between $\frac{1}{2}$ and $1$.

Indeed, $I \times I$ is not convex because $(0.5, 50)$ lies in the interval $((0.5, 0.5), (1, 0.5))$, where $(0.5, 0.5), (1, 0.5) \in I \times I$, but $(0.5, 50) \notin I \times I$.

(The set $I \times I$ in the dictionary order topology is called the ordered square, denoted by $I_o^2$.)

info

To avoid ambiguity, whenever $X$ is an ordered set in the order topology and $Y$ is a subset of $X$, we shall assume that $Y$ is given the subspace topology unless specifically stated otherwise.

Product Topology (+ Box Topology)

Forming new topologies from old ones.

Product Topology on $X \times Y$

Definition. Let $X$ and $Y$ be topological spaces. The product topology on $X \times Y$ is the topology generated by the collection $\mathcal{B}$ of all sets of the form $U \times V$ as the basis, where $U$ is an open subset of $X$ and $V$ is an open subset of $Y$.

Check that the collection $\mathcal{B}$ is a basis.

1. Indeed, $X \times Y$ is a basis element ($X$ and $Y$ themselves open), and they contain all of the elements of $X \times Y$.

2. The intersection of any two basis elements $U_1 \times V_1$ and $U_2 \times V_2$ is another basis element, since $(U_1 \times V_1) \cap (U_2 \times V_2) = (U_1 \cap U_2) \times (V_1 \cap V_2)$.

warning

Note that the collection $\mathcal{B}$ itself is not a topology on $X \times Y$, but it is open in $X \times Y$.

[Theorem 15.1] If $\mathcal{B}$ is a basis for the topology of $X$ and $\mathcal{C}$ is a basis for the topology of $Y$, then the collection

$$\mathcal{D} = \{ B \times C : B \in \mathcal{B} \text{ and } C \in \mathcal{C}\}$$

is a basis for the topology of $X \times Y$.

Definition. Define the projections $\pi_1 : X \times Y \to X$ by $\pi_1(x,y)=x$ and $\pi_2 : X \times Y \to Y$ by $\pi_2(x,y)=y$.

It follows that $\pi_1^{-1}(U)$ where $U$ is open in $X$ is $U \times Y$ and $\pi_2^{-1}(V)$ where $V$ is open in $Y$ is $X \times V$, so $\pi_1^{-1}(U) \cap \pi_2^{-1}(V) = U \times V$.

[Theorem 15.2] The collection

$$\mathcal{S} = \{\pi_1^{-1}(U) : U \text{ open in } X\} \cup \{ \pi_2^{-1}(V) : V \text{ open in } Y\}$$

is a subbasis for the product topology on $X \times Y$.

Product Topology in General + Box Topology

There are two possible ways to define a product topology on more general Cartesian products with finite or infinite dimensions, i.e. Cartesian products in the form of $X_1 \times \cdots \times X_n$ and $X_1 \times X_2 \times \cdots$, where each $X_i$ is a topological space, which are the following:

1. Box topology: topology generated by taking as basis all sets of the form $U_1 \times \cdots \times U_n$ in the first case, and of the form $U_1 \times U_2 \times \cdots$ in the second case, where $U_i$ is an open set of $X_i$ for each $i$.
2. Product topology: topology generated by taking as a subbasis all sets of the form $\pi_i^{-1}(U_i)$ (recall that $\pi_i$ represents the projection function), where $i$ is any index and $U_i$ is an open set of $X_i$.

How do these topologies differ? Let $B$ be a basis element for the second topology, then it is a finite intersection of subbasis elements $\pi_1^{-1}(U_i)$, say for $i = i_1, \ldots, i_k$, then a point $\mathbf{x}$ belongs to $B$ if and only if $\pi_i(\mathbf{x})$ belongs to $U_i$ for $i=i_1,\ldots,i_k$; there is no restriction on $\pi_i(\mathbf{x})$ for other values of $i$.

It follows that the two topologies above agree for the finite Cartesian product but differ for the infinite product.

Now, we shall introduce a more general notion of Cartesian products, which are formed by a family of sets indexed by an arbitrary set, instead of a subset of $\mathbb{Z}_+$.

Definition. (Tuples with arbitrary index). Let $J$ be an index set. Given a set $X$, we define a $J$-tuple of elements of $X$ to be a function $\mathbf{x} : J \to X$. If $\alpha$ is an element of $J$, we often denote the value of $\mathbf{x}$ at $\alpha$ by $x_\alpha$ rather than $\mathbf{x}(\alpha)$; we call the the $\alpha$-th coordinate of $\mathbf{x}$. We also often denote the function $\mathbf{x}$ itself by the symbol $(x_\alpha)_{\alpha \in J}$, which is as close as we can come to a 'tuple notation' for an arbitrary index set $J$. We denote the set of all $J$-tuple of elements of $X$ by $X^J$.

Definition. (Cartesian products with arbitrary index). Let $\{A_\alpha\}_{\alpha \in J}$ be an indexed family of sets; let $X = \bigcup_{\alpha \in J}A_\alpha$. The Cartesian product of this indexed family, denoted by $\prod_{\alpha \in J}A_\alpha$, is defined to be the set of all $J$-tuples $(x_\alpha)_{\alpha \in J}$ of elements of $X$ such that $x_\alpha \in A_\alpha$ for each $\alpha \in J$, i.e. it is the set of all functions $\mathbf{x} : J \to \bigcup_{\alpha \in J}A_\alpha$ such that $\mathbf{x}(\alpha) \in A_\alpha$ for each $\alpha \in J$.

note

If such Cartesian product is formed by an indexed family such that all its component sets are non-empty, the assertion that this Cartesian product is non-empty, i.e. there exists such function $\mathbf{x}$, is equivalent to the Axiom of Choice.

A proof of this equivalence is a solution to Exercise 19.9.

Definition. (Box topology for arbitrarily indexed Cartesian products). Let $\{X_\alpha\}_{\alpha \in J}$ be an indexed family of topological spaces. Let us take as a basis for a topology on the product space $\prod_{\alpha \in J}X_\alpha$ the collection of all sets of the form $\prod_{\alpha \in J}U_\alpha$, where $U_\alpha$ is open in $X_\alpha$, for each $\alpha \in J$. The topology generated by this basis is called the box topology.

Definition. (Projection mapping for arbitrarily indexed Cartesian products). Generalising the subbasis formulation of the definition, we call the function $\pi_\beta : \prod_{\alpha \in J}X_\alpha \to X_\beta$ that assigns to each element of the product space its $\beta$-th coordinate, i.e. $\pi_\beta((x_\alpha)_{\alpha \in J})=x_\beta$ the projection mapping associated with the index $\beta$.

Definition. (Product topology and product spaces for arbitrarily indexed Cartesian products). Let $\mathcal{S}_\beta$ denote the collection $\mathcal{S}_\beta=\{ \pi_\beta^{-1}(U_\beta) : U_\beta \text{ open in } X_\beta\}$, and let $\mathcal{S}$ denote the union of these collections, i.e. $\mathcal{S}=\bigcup_{\beta \in J}\mathcal{S}_\beta$. The topology generated by the subbasis $\mathcal{S}$ is called the product topology. In this topology $\prod_{\alpha \in J}X_\alpha$ is called a product space.

[Theorem 19.1] (Comparison of the box and product topologies). The box topology on $\prod X_\alpha$ has as basis all sets of the form $\prod U_\alpha$, where $U_\alpha$ is open in $X_\alpha$ for each $\alpha$. The product topology on $\prod X_\alpha$ has as basis all sets of the form $\prod U_\alpha$, where $U_\alpha$ is open in $X_\alpha$ for each $\alpha$ and $U_\alpha$ equals $X_\alpha$ except for finitely many values of $\alpha$.

Consider the basis $\mathcal{B}$ that $\mathcal{S}$ (as defined above) generates. The collection $\mathcal{B}$ consists of all finite intersections of elements of $\mathcal{S}$. We consider two cases.

Case I: the elements in the intersection belong to the same one of the sets $\mathcal{S}_\beta$. We then do not get anything new, because

$$\pi_\beta^{-1}(U_\beta) \cap \pi_\beta^{-1}(V_\beta) = \pi_\beta^{-1}(U_\beta \cap V_\beta)=\pi_\beta^{-1}(U_\beta \cap V_\beta)$$

is still an element of $\mathcal{S}_\beta$. The same applies for finitely many elements of $\mathcal{S}_\beta$.

Case II: the elements in the intersection come from different sets in $\mathcal{S}_\beta$. The typical element of the basis $\mathcal{B}$ can then be described as follows: Let $\beta_1, \ldots, \beta_n$ be a finite set of distinct indices from the index set $J$, and let $U_{\beta_i}$ be an open set in $X_{\beta_i}$ for $i=1,\ldots,n$, then

$$B=\pi_{\beta_1}^{-1}(U_{\beta_1}) \cap \pi_{\beta_2}^{-1}(U_{\beta_2}) \cap \cdots \cap \pi_{\beta_n}^{-1}(U_{\beta_n})$$

is also the typical element of $\mathcal{B}$.

Now, a point $\mathbf{x}=(x_\alpha)$ is in $B$ if and only if its $\beta_1$-th coordinate is in $U_{\beta_1}$, its $\beta_2$-th coordinate is in $U_{\beta_2}$, and so on. There is no restriction whatsoever on the $\alpha$-th coordinate of $\mathbf{x}$ if $\alpha$ is not one of the indices $\beta_1,\ldots,\beta_n$. Hence, we can write $B$ as the product

$$B=\prod_{\alpha \in J}U_\alpha$$

where $U_\alpha$ denotes the entire space $X_\alpha$ if $\alpha \neq \beta_1,\ldots,\beta_n$.

info

Since a number of key theorems about finite products will also hold for arbitrary products if we use the product topology, but note if we use the box topology, whenever we consider the product $\prod X_\alpha$, we shall assume it is given the product topology unless specifically stated otherwise.

• [Theorem 19.2] (Basis inheritance). Suppose the topology on each space $X_\alpha$ is given by a basis $\mathcal{B}_\alpha$, then the collection of all sets of the form $\prod_{\alpha \in J}B_\alpha$, where $B_\alpha \in \mathcal{B}_\alpha$ for each $\alpha$, will serve as a basis for the box topology on $\prod_{\alpha \in J} X_\alpha$.

  The collection of all sets of the same form, where $B_\alpha \in \mathcal{B}_\alpha$ for finitely many indices $\alpha$ and $B_\alpha = X_\alpha$ for all the remaining indices, will serve as a basis for the product topology $\prod_{\alpha \in J}X_\alpha$.

• [Theorem 19.3] (Subspace inheritance). Let $A_\alpha$ be a subspace of $X_\alpha$, for each $\alpha \in J$, then $\prod A_\alpha$ is a subspace of $\prod X_\alpha$ if both products are given the box topology, or if both products are given the product topology.

• [Theorem 19.4] (Hausdorff inheritance) If each space $X_\alpha$ is Hausdorff, then $\prod X_\alpha$ is a Hausdorff space in both the box and product topologies.

• [Theorem 19.5] (Closure inheritance). Let $\{X_\alpha\}$ be an indexed family of spaces; let $A_\alpha \subseteq X_\alpha$ for each $\alpha$. If $\prod X_\alpha$ is given either the product or the box topology, then

$$\prod \overline{A_\alpha}=\overline{\prod A_\alpha}.$$

The proofs of Theorems 19.2, 19.3 and 19.4 are given in a solution to Exercises 19.1, 19.2 and 19.3 respectively.

Proof of Theorem 19.5.

Let $\mathbf{x}=(x_\alpha)$ be a point of $\prod \overline{A_\alpha}$. We show that $\mathbf{x} \in \overline{\prod A_\alpha}$. Let $U = \prod U_\alpha$ be a basis element for either the box or product topology that contains $\mathbf{x}$. Since $x_\alpha \in \overline{A_\alpha}$, we can chooise a point $y_\alpha \in U_\alpha \cap A_\alpha$ for each $\alpha$ (see Theorem 17.5 below). Then $\mathbf{y}=(y_\alpha)$ belongs to both $U$ and $\prod A_\alpha$. Since $U$ is arbitrary, it follows that $\mathbf{x}$ belongs to the closure of $\prod A_\alpha$.

Conversely, suppose $\mathbf{x}=(x_\alpha)$ lies in the closure of $\prod A_\alpha$, in either topology. We show that for any given index $\beta$, we have $x_\beta \in \overline{A_\beta}$. Let $V_\beta$ be an arbitrary open set of $X_\beta$ containing $x_\beta$. Since $\pi_\beta^{-1}(V_\beta)$ is open in $\prod X_\alpha$ in either topology, it contains a point $\mathbf{y}=(y_\alpha)$ of $\prod A_\alpha$. Then $y_\beta$ belongs to $V_\beta \cap A_\beta$. It follows that $x_\beta \in \overline{A_\beta}$.

[Theorem 19.6] (Continuity inheritance). Let $f: A \to \prod_{\alpha \in J} X_\alpha$ be given by the equation

$$f(a)=(f_\alpha(a))_{\alpha \in J},$$

where $f_\alpha : A \to X_\alpha$ for each $\alpha$. Let $\prod X_\alpha$ have the product topology. Then the function $f$ is continuous if and only if each function $f_\alpha$ is continuous.

warning

Theorem 19.6 fails if we apply the box topology. A counterexample is given as follows:

Consider $\mathbb{R}^{\omega}$, the countably infinite product of $\mathbb{R}$ with itself. Recall that $\mathbb{R}^{\omega}=\prod_{n \in \mathbb{Z}_+} \mathbb{R}$.

Define a function $f : \mathbb{R} \to \mathbb{R}^{\omega}$ by the equation

$$f(t)=(t,t,t,\ldots);$$

the $n$-th coordinate function of $f$ is the function $f_n(t)=t$, i.e. $f_n=\pi_n \circ f$. Each of the coordinate functions $f_n : \mathbb{R} \to \mathbb{R}$ is continuous, but $f$ is not continuous if $\mathbb{R}^{\omega}$ is given the box topology.

Consider, for example, the basis element $\prod_{n \in \mathbb{Z}_+}\left(-\frac{1}{n},\frac{1}{n}\right)$ for the box topology (which is certainly an open subset of $\mathbb{R}^{\omega}$). We assert that $f^{-1}(B)$ is not open in $\mathbb{R}$. If $f^{-1}(B)$ were open in $\mathbb{R}$, it would contain some interval $(-\delta,\delta)$ ($\delta > 0$) about the point $0$ (because $(0,0,0,\ldots) \in B$). This would mean that $f((-\delta,\delta)) \subseteq B$, so that, by applying $\pi_n$ to both sides of the inclusion, we have

$$f_n((-\delta,\delta)) = (-\delta,\delta) \subseteq \left(-\frac{1}{n},\frac{1}{n}\right)$$

for all $n$, which is a contradiction as it is impossible.

Metric Topology

Definition. A metric on a set $X$ is a function $d : X \times X \to \mathbb{R}$ having the following properties:

1. (Positive definite) $d(x,y) \geqslant 0$ for all $x,y \in X$; equality holds if and only if $x = y$.
2. (Symmetry) $d(x,y)=d(y,x)$ for all $x,y \in X$.
3. (Triangle inequality) $d(x,y) + d(y,z) \geqslant d(x,z)$, for all $x, y, z \in X$.

The number $d(x,y)$, where $d$ is a metric on $X$, is often called the distance between $x$ and $y$ in the metric $d$.

Given $\varepsilon > 0$, the set $B_d(x, \varepsilon) := \{ y : d(x,y)<\varepsilon\}$ is called the $\varepsilon$-ball centred at $x$.. When no confusion arises, the subscript $d$ can be omitted.

Definition. If $d$ is a metric on the set $X$, then the collection of all $\varepsilon$-balls $B_d(x,\varepsilon)$, for $x \in X$ and $\varepsilon>0$, is a basis for the topology on $X$, called the metric topology induced by $d$.

The definition of the metric topology can be rephrased as follows:

A set $U$ is open in the metric topology induced by $d$ if and only if for each $y \in U$, there is a $\delta>0$ such that $B_d(y, \delta) \subseteq U$.

Definition. If $X$ is a topological space, $X$ is said to be metrizable if there exists a metric $d$ on the set $X$ that induces the topology of $X$. A metric space is a metrizable space $X$ together with a specific metric $d$ that gives the topology of $X$.

Many important topological spaces are metrizable, but some are not.

note

For example, $\mathbb{R}$ with the order topology is metrizable. Indeed, the Euclidean metric $d(x,y) := |x-y|$ is the metric that induces the topology. To see this, note that each basis element $(a,b)$ for the order topology is a basis element for the metric topology; indeed, $(a,b)=B(x,\varepsilon)$ where $x = (a+b)/2$ and $\varepsilon=(b-a)/2$. Conversely, each $\varepsilon$-ball $B(x,\varepsilon)$ equals an open interval: the interval $(x-\varepsilon,x+\varepsilon)$.

A discrete topology is also metrizable. It can be induced by the discrete metric, defined by $d(x,y)=\begin{cases} 1 & \text{if } x \neq y, \\ 0 & \text{if } x=y \end{cases}$.

Definition. Let $X$ be a metric space with metric $d$. A subset $A$ of $X$ is said to be bounded if there is some number $M$ such that $d(a_1,a_2) \leqslant M$ for every pair $a_1,a_2$ of points of $A$.

If $A$ is bounded and non-empty, the diameter of $A$ is defined to be the number $\text{diam } A = \sup\{d(a_1,a_2) : a_1,a_2 \in A\}$.

[Theorem 20.1] Let $X$ be a metric space with metric $d$. Define $\bar{d} : X \times X \to \mathbb{R}$ by the equation $\bar{d}(x,y)=\min\{d(x,y),1\}$, then $\bar{d}$ is a metric that induces the same topology as $d$.

The metric $\bar{d}$ is called the standard bounded metric corresponding to $d$.

Definition. Given $\mathbf{x} = (x_1,\ldots,x_n)$ in $\mathbb{R}^n$, we define the norm of $\mathbf{x}$ by the equation

$$\Vert\mathbf{x}\Vert=(x_1^2+\cdots+x_n^2)^{\frac{1}{2}};$$

we define the Euclidean metric $d$ on $\mathbb{R}^n$ by the equation

$$d(\mathbf{x},\mathbf{y})=\Vert\mathbf{x}-\mathbf{y}\Vert=[(x_1-y_1)^2+\cdots+(x_n-y_n)^2]^{\frac{1}{2}}.$$

We define the square metric $\rho$ by the equation

$$\rho(\mathbf{x},\mathbf{y})=\max\{|x_1-y_1|,\ldots,|x_n-y_n|\}.$$

[Lemma 20.2] Let $d$ and $d'$ be two metrics on the set $X$; let $\mathcal{T}$ and $\mathcal{T}'$ be the topologies they induce, respectively. Then $\mathcal{T}'$ is finer than $\mathcal{T}$ if and only if for each $x$ in $X$ and each $\varepsilon>0$, there exists $\delta>0$ such that $B_{d'}(x,\delta) \subseteq B_d(x,\varepsilon)$.

[Theorem 20.3] The topologies on $\mathbb{R}^n$ induced by the Euclidean metric $d$ and the square metric $\rho$ are the same as the product topology on $\mathbb{R}^n$.

Let $\mathbf{x}=(x_1,\ldots,x_n)$ and $\mathbf{y}=(y_1,\ldots,y_n)$ be two points of $\mathbb{R}^n$. By algebraic manipulation, we obtain that

$$\rho(\mathbf{x},\mathbf{y}) \leqslant d(\mathbf{x},\mathbf{y}) \leqslant \sqrt{n}\rho(\mathbf{x},\mathbf{y}).$$

note

In other words, the metrics $d$ and $\rho$ are (topologically) equivalent. In fact, as shown above, these two particular metrics are strongly equivalent, which implies topological equivalence.

The first inequality shows that $B_d(\mathbf{x},\varepsilon) \subseteq B_\rho(\mathbf{x},\varepsilon)$ whereas the second equality shows that $B_\rho(\mathbf{x},\varepsilon/n) \subseteq B_d(\mathbf{x},\varepsilon)$.

Now, we show that the product topology is the same as that given by the metric $\rho$. First, let

$$B=(a_1,b_1) \times \cdots \times (a_n,b_n)$$

be a basis element for the product topology, and let $\mathbf{x}=(x_1,\ldots,x_n)$ be and element of $B$. For each $i$, there is an $\varepsilon_i$ such that

$$(x_i-\varepsilon_i, x_i+\varepsilon_i) \subseteq (a_i,b_i);$$

choose $\varepsilon = \min\{\varepsilon_1,\ldots,\varepsilon_n\}$. Then $B_\rho(\mathbf{x},\varepsilon) \subseteq B$, since if $\mathbf{y} \in B_\rho(\mathbf{x},\varepsilon)$, then the maximum of $|y_i-x_i|$ is less than $\varepsilon$, which implies that $x_i-\varepsilon < y_i < x_i+\varepsilon$ for each $i$; since $\varepsilon \leqslant \varepsilon_i$ for each $i$, it follows that $y_i \in (x_i-\varepsilon_i,x_i+\varepsilon_i) \subseteq (a_i,b_i)$ for each $i$, so $\mathbf{y} \in B$. As a result, the $\rho$-topology is finer than the product topology.

Conversely, let $B_\rho(\mathbf{x},\varepsilon)$ be a basis element for the $\rho$-topology. Given the element $\mathbf{y} \in B_\rho(\mathbf{x},\varepsilon)$, we need to find a basis element $B$ for the product topology such that $\mathbf{y} \in B \subseteq B_\rho(\mathbf{x},\varepsilon)$, and this is immediate: we can just take $B=B_\rho(\mathbf{x},\varepsilon)$, which itself is a basis element for the product topology.

Now we consider the infinite Cartesian product $\mathbb{R}^\omega$. It is natural to try generalising the metrics $d$ and $\rho$ to this space in the following ways:

$$d(x,y)=\left[\sum_{i=1}^{\infty}(x_i-y_i)^2\right]^{\frac{1}{2}} \tag{1}$$ $$\rho(x,y)=\sup_{n \in \mathbb{Z}_+}\{|x_n-y_n|\} \tag{2}$$

but both of the equations above do not always make sense, though equation (1) does define a metric on a certain important subset of $\mathbb{R}^\omega$ (see Exercise 20.10), whereas equation (2) makes sense when the metric is replaced by the standard bounded metric.

Definition. Given an index set $J$, and given points $\mathbf{x}=(x_\alpha)_{\alpha \in J}$ and $\mathbf{y}=(y_\alpha)_{\alpha \in J}$ of $\mathbb{R}^J$, let us define a metric $\bar{\rho}$ on $\mathbb{R}^J$ by the equation

$$\bar{\rho}(\mathbf{x},\mathbf{y})=\sup\{\bar{d}(x_\alpha,y_\alpha) : \alpha \in J \},$$

where $\bar{d}$ is the standard bounded metric on $\mathbb{R}$. One can check that $\bar{\rho}$ is indeed a metric; it is called the uniform metric on $\mathbb{R}^J$, and the topology it induces is called the uniform topology.

[Theorem 20.4] The uniform topology on $\mathbb{R}^J$ is finer than the product topology and coarser than the box topology; these theree topologies are all different if $J$ is infinite.

[Theorem 20.5] Let $\bar{d}(a,b)=\min\{|a-b|,1\}$ be the standard bounded metric on $\mathbb{R}$. If $\mathbf{x}$ and $\mathbf{y}$ are two points of $\mathbb{R}^\omega$, define

$$D(\mathbf{x},\mathbf{y})=\sup\left\{\frac{\overline{d}(x_i,y_i)}{i}\right\}.$$

Then $D$ is a metric that induces the product topology on $\mathbb{R}^\omega$.

note

Theorem 20.5 shows that if $J$ is infinite, then $\mathbb{R}^J$ is metrizable if and only if $J$ is countable and $\mathbb{R}^J$ has the product topology.

Now, we consider the relation of the metric topology to other topological concepts:

• Subspaces or metric spaces behave as expected: if $A$ is a subspace of the topological space $X$ and $d$ is a metric for $X$, then the restriction of $d$ to $A \times A$ is a metric for the topology of $A$. A proof of this is shown in Exercise 21.1.
• There is not much to be said regarding order topologies; some are metrizable, some are not.
• The Hausdorff axiom is satisfied by every metric topology. Indeed, if $x$ and $y$ are distinct points of the metric space $(X,d)$, then we let $\varepsilon=\frac{d(x,y)}{2}$; the triangle inequality implies that $B_d(x,\varepsilon)$ and $B_d(y, \varepsilon)$ are disjoint.
• For product topologies, Theorem 20.5 shows that countable products of metrizable spaces are metrizable. A proof of this is given in Exercise 21.3.
• For continuous functions, the familiar '$\varepsilon$-$\delta$ definition' of continuity carries over to general metric spaces, and so does the sequential criterion. We can also see that we can construct continuous functions through 'arithmetic operations' or by applying uniform limit theorem.

[Theorem 20.1] Let $f : X \to Y$; let $X$ and $Y$ be metrizable with metrics $d_X$ and $d_Y$, respectively. Then continuity of $f$ is equivalent to the requirement that given $x \in X$ and given $\varepsilon>0$, there exists $\delta>0$ such that

$$d_X(x,y) \implies d_Y(f(x),f(y))<\varepsilon.$$

[Lemma 21.2] (The sequence lemma). Let $X$ be a topological space; let $A \subseteq X$. If there is a sequence of points of $A$ converging to $x$, then $x \in \overline{A}$; the converse holds if $X$ is metrizable.

Suppose that $x_n \to x$, where $x_n \in A$, then every neighbourhood $U$ of $x$ contains a point of $A$, so $x \in \overline{A}$ by Theorem 17.5.

Conversely, suppose that $x$ is metrizable and $x \in \overline{A}$. Let $d$ be a metric for the topology of $X$. For each positive integer $n$, take the neighbourhood $B_d(x,1/n)$ centred at $x$ and of radius $1/n$. Choose $x_n$ to be a point of its intersection with $A$. We assert that the sequence $x_n$ converges to $x$: note that any open set $U$ containing $x$ contains an $\varepsilon$-ball $B_d(x,\varepsilon)$ centred at $x$, so if we choose $N$ so that $1/N<\varepsilon$ (possible by Archimedean property), then $U$ contains $x_i$ for all $i \geqslant N$.

[Theorem 21.3] (Sequential criterion of continuity). Let $f : X \to Y$. If the function $f$ is continuous, then for every convergent sequence $x_n \to x$ in $X$, the sequence $f(x_n)$ converges to $f(x)$. The converse holds if $X$ is metrizable.

Suppose that $f$ is continuous. Given $x_n \to x$, we wish to show that $f(x_n) \to f(x)$. Let $V$ be a neighbourhood of $f(x)$, then $f^{-1}(V)$ is a neighbourhood of $x$, so there is an $N$ such that $x_n \in f^{-1}(V)$ for $n \geqslant N$, thus $f(x_n) \in V$ for $n \geqslant N$.

Conversely, assume that the convergent sequence condition is satisfied. Let $A$ be a subset of $X$; we show that $f(\overline{A}) \subseteq \overline{f(A)}$ (which is equivalent to continuity by Theorem 18.1). If $x \in \overline{A}$, then there is a sequence $x_n$ of points of $A$ converging to $x$ (by Lemma 21.2). By assumption, the sequence $f(x_n)$ converges to $f(x)$. Since $f(x_n) \in f(A)$, Lemma 21.2 implies that $f(x) \in \overline{f(A)}$ (Note that the metrizability of $Y$ is not needed.) Hence $f(\overline{A}) \subseteq \overline{f(A)}$, as desired.

info

Incidentally, in the proof of Lemma 21.2 and Theorem 21.3, we only required the countable collection $B_d(x,1/n)$ of balls about $x$ instead of using the full strength of metrizability. This leads us to make a new definition.

A space $X$ is said to have a countable basis at the point $x$ if there is a countable collection $\{U_n\}_{n \in \mathbb{Z}_+}$ of neighbourhoods of $x$ such that any neighbourhood $U$ of $x$ contains at least one of the sets $U_n$. A space $X$ that has a countable basis at each of its points is said to satisfy the first countability axiom.

A metrizable space always satisfies the first countability axiom, but the converse is not true.

[Lemma 21.4] The addition, subtraction and multiplication operations are continuous functions from $\mathbb{R} \times \mathbb{R}$ into $\mathbb{R}$; the quotient operation is a continuous function from $\mathbb{R} \times (\mathbb{R} \backslash \{0\})$ into $\mathbb{R}$.

A proof of this lemma is a solution to Exercise 21.12.

[Theorem 21.5] ('Arithmetic operations' on continuous functions). If $X$ is a topological space, and if $f,g : X \to \mathbb{R}$ are continuous functions, then $f + g$, $f - g$, and $f \cdot g$ are continuous. If $g(x) \neq 0$ for all $x$, then $f/g$ is continuous.

The map $h : X \to \mathbb{R} \times \mathbb{R}$ defined by

$$h(x) = (f(x),g(x))$$

is continuous, by Theorem 18.4 (see below). The function $f + g$ equals the composite of $h$ and the addition operation $+ : \mathbb{R} \times \mathbb{R} \to \mathbb{R}$, which we know is continuous by Lemma 21.4, thus $f+g$ is continuous. Similar arguments apply to $f-g$, $f \cdot g$ and $f/g$.

Definition. Let $f_n : X \to Y$ be a sequence of functions from the set $X$ to the metric space $Y$. Let $d$ be the metric for $Y$. We say that the sequence $(f_n)$ converges uniformly to the function $f : X \to Y$ if given $\varepsilon > 0$, there exists an integer $N$ such that $d(f_n(x),f(x))<\varepsilon$ for all $n > N$ and all $x$ in $X$.

note

Contrast this uniform convergence with pointwise convergence, for which the integer $N$ for the corresponding $\varepsilon$ may vary depending on the choice of $x \in X$.

Exercise 21.6 provides an example of a sequence of functions that is pointwise convergent but not uniformly convergent.

[Theorem 21.6] (Uniform limit theorem). Let $f_n : X \to Y$ be a sequence of continuous functions from the topological space $X$ to the metric space $Y$. If $(f_n)$ converges uniformly to $f$, then $f$ is continuous.

Let $V$ be an open set in $Y$, and $x_0$ be a point of $f^{-1}(V)$. We want to find a neighbourhood $U$ of $x_0$ such that $f(U) \subseteq V$ (see Theorem 18.1).

The idea of finding such neighbourhood $U$ is by using the uniform convergence of $(f_n)$ to $f$ (twice) and the continuity of each $f_n$.

Let $y_0=f(x_0)$. First choose $\varepsilon$ so that the $\varepsilon$-ball $B(y_0,\varepsilon)$ is contained in $V$. Next, using uniform convergence, choose $N$ so that for all $n \geqslant N$ and for all $x \in X$,

$$d(f_n(x),f(x))<\varepsilon/3.$$

Finally, using continuity of $f_N$, take a neighbourhood $U$ of $x_0$ such that for any $x \in U$, we have

$$d(f_N(x),f_N(x_0))<\varepsilon/3.$$

We claim that $f$ carries $U$ into $B(y_0,\varepsilon)$ and hence into $V$. Note that if $x \in U$, then

$$d(f(x),f_N(x))<\varepsilon/3$$$$d(f_N(x),f_N(x_0))<\varepsilon/3$$$$d(f_N(x_0),f(x_0))<\varepsilon/3$$

Adding them together and applying triangle inequality, we see that $d(f(x),f(x_0))<\varepsilon$, as desired.

info

Examples of spaces that are not metrizable:

• $\mathbb{R}^\omega$ in the box topology.
• An uncountable product of $\mathbb{R}$ with itself.

Quotient Topology

A torus is an example of a quotient topology which arises from the Cartesian plane, or the unit square.

Definition. Let $X$ and $Y$ be topological spaces; let $p : X \to Y$ be a surjective map. The map $p$ is said to be a quotient map provided a subset $U$ of $Y$ is open in $Y$ if and only if $p^{-1}(U)$ is open in $X$.

note

Note that the implication is two-sided compared to the continuity definition, which indicates that this condition is stronger than continuity. An equivalent condition is that a subset $A$ of $Y$ is closed in $Y$ if and only if $p^{-1}(A)$ is closed in $X$; such equivalence follows from the fact that $f^{-1}(Y \backslash B)= f^{-1}(Y) \backslash f^{-1}(B) = X \backslash f^{-1}(B)$.

We can also decsribe quotient maps in the following way: We say that a subset $C$ of $X$ is saturated (with respect to the surjective map $p : X \to Y$) if $C$ contains every set $p^{-1}(\{y\})$ that it intersects (i.e. for those $p^{-1}(\{y\})$ that has a non-empty intersection with $C$, we have that $p^{-1}(y)$ is a subset of $C$). Hence $C$ is saturated if it equals the complete inverse image of a subset of $Y$. Saying that $p$ is a quotient map is equivalent to saying that $p$ is continuous and $p$ maps saturated open sets of $X$ to open sets of $Y$ (or saturated closed sets of $X$ to closed sets of $Y$).

Two special kinds of quotient maps are the open maps and the closed maps.

[A map $f : X \to Y$ is said to be an open map if for each open set $U$ of $X$, the set $f(U)$ is open in $Y$. It is said to be a closed map if for each closed set $A$ of $X$, the set $f(A)$ is closed in $Y$.]

It follows from the definition that if $p : X \to Y$ is a surjective continuous map that is either open or closed, then $p$ is a quotient map.

There are quotient maps that are neither open nor closed. See Exercise 22.3 for a proof.

Definition. If $X$ is a space and $A$ is a set and if $p : X \to A$ is a surjective map, then there exists exactly one topology $\mathcal{T}$ on $A$ relative to which $p$ is a quotient map; it is called the quotient topology induced by $p$, and is defined by letting it consist of those subsets $U$ of $A$ such that $p^{-1}(U)$ is open in $X$.

A special case in which the quotient topology occurs particularly often is given as follows:

Definition. Let $X$ be a topological space, and let $X^*$ be a partition of $X$ into disjoint subsets whose union is $X$. Let $p : X \to X^*$ be the surjective map that carries each point of $X$ to the element of $X^*$ containing it. In the quotient topology induced by $p$, the space $X^*$ is called a quotient space of $X$.

info

Given $X^*$, there is an equivalence relation of which the elements of $X^*$ are the equivalence classes. One can think of $X^*$ as having been obtained by 'identifying' each pair of equivalent points. For this reason, the quotient space $X^*$ is often called an identification space, or a decomposition space, of the space $X$.

(With respect to the corresponding equivalence relation $\sim$, the space $X^*$ can also be notated as $X/\sim$.)

We can also describe the topology of $X^*$ in another way. A susbet $U$ of $X^*$ is a collection of equivalence classes, and the set $p^{-1}(U)$ is just the union of the equivalence classes belonging to $U$. Thus, the typical open set of $X^*$ is a collection of equivalence classes whose union is an open set of $X$.

[Theorem 22.1] Let $p : X \to Y$ be a quotient map; let $A$ be a subspace of $X$ that is saturated with respect to $p$; let $q : A \to p(A)$ be the map obtained by restricting $p$.

1. If $A$ is either open or closed in $X$, then $q$ is a quotient map.
2. If $p$ is either an open map or a closed map, then $q$ is a quotient map.

[Theorem 22.2] Let $p : X \to Y$ be a quotient map. Let $Z$ be a space and let $g : X \to Z$ be a map that is constant on each set $p^{-1}(\{y\})$, for $y \in Y$. Then $g$ induces a map $f : Y \to Z$ such that $f \circ p = g$. THe induced map $f$ is continuous if and only if $g$ is continuous; $f$ is a quotient map if and only if $g$ is a quotient map.

[Corollary 22.3] Let $g : X \to Z$ be a surjective continuous map. Let $X^*$ be the following collection of subsets of $X$:

$$X^* = \{g^{-1}(\{z\}) : z \in Z\}.$$

Give $X^*$ the quotient topology.

(a) The map $g$ induces a bijective continuous map $f : X^* \to Z$, which is a homeomorphism if and only if $g$ is a quotient map.

Corollary 22.3(a) is also known as the universal property of quotient spaces.

(b) If $Z$ is Hausdorff, so is $X^*$.

note

Corollary 22.3(a) is analogous to the first isomorphism theorem (a.k.a. fundamental theorem on homomorphisms or universal property of quotient groups) in group theory.

warning

(Example 7).

The product of two quotient maps need not be a quotient map. Here is an example (that is nicer).

Let $X = \mathbb{R}$ and let $X^*$ be the quotient space obtained from $X$ by identifying the subset $\mathbb{Z}_+$ to a point $b$; let $p : X \to X^*$ be the quotient map. Let $\mathbb{Q}$ be the subspace of $\mathbb{R}$ consisting of the rational numbers; let $i : \mathbb{Q} \to \mathbb{Q}$ be the identity map. We show that

$$p \times i : X \times \mathbb{Q} \to X^* \times \mathbb{Q}$$

is not a quotient map.

For each $n$, let $c_n=\sqrt{2}/n$, and consider the straight lines in $\mathbb{R}^2$ with gradients 1 and -1, respectively, through the point $(n,c_n)$. Let $U_n$ consist of all points $X \times \mathbb{Q}$ that lie above both of these lines or beneath both of them, and also between the vertical lines $x=n-\frac{1}{4}$ and $x= n+\frac{1}{4}$. Then $U_n$ is open in $X \times \mathbb{Q}$, it contains the set $\{n\} \times \mathbb{Q}$ because $c_n$ is not rational.

Let $U$ be the union of the sets $U_n$, then $U$ is open in $X \times \mathbb{Q}$. It is saturated with respect to $p \times i$ because it contains the entire set $\mathbb{Z}_+ \times \{q\}$ for each $q \in \mathbb{Q}$. We assume that $U'=(p \times i)(U)$ is open in $X^* \times \mathbb{Q}$ and reach a contradiction.

Since $U$ contains, in particular, the set $\mathbb{Z}_+ \times \{0\}$, the set $U'$ contains the point $(b,0)$. Hence $U'$ contains an open set of the form $W \times I_\delta$, where $W$ is a neighbourhood of $b$ in $X^*$ and $I_\delta := \{y \in \mathbb{Q} : |y|<\delta\}$. It follows that

$$p^{-1}(W) \times I_\delta \subseteq U.$$

Choose $n$ large enough so that $c_n < \delta$, then since $p^{-1}(W)$ is open in $X$ and contains $\mathbb{Z}_+$, we can choose $\varepsilon < \frac{1}{4}$ so that the interval $(n-\varepsilon,n+\varepsilon)$ is contained in $p^{-1}(W)$, then $U$ contains the subset $V = (n-\varepsilon,n+\varepsilon) \times I_\delta$ of $X \times \mathbb{Q}$. However, there are many points $(x,y)$ of $V$ that do not lie in $U$ (e.g. the points $(x,y)$ where $x = n+\frac{1}{2}\varepsilon$ and $y$ is a rational number with $|y-c_n|<\frac{1}{2}\varepsilon$.)!

Closed Sets and Limit Points

Closed Sets, Interior, Closure, Neighbourhood

Definition. A subset $A$ of a topological space $X$ is said to be closed if the set $X \backslash A**$ is open.

[Theorem 17.1] Let $X$ be a topological space, then the following hold:

1. $\emptyset$ and $X$ are closed.
2. Arbitrary intersections of closed sets are closed.
3. Finite unions of closed sets are closed.

The proof for 1. follows from the (topological) definition of openness and the facts that $\emptyset = X \backslash X$ and $X = X \backslash \emptyset$. The proofs for 2. and 3. follow from the definition of a closed set and de Morgan's law.

[Theorem 17.2] Let $Y$ be a subspace of $X$, then a set $A$ is closed in $Y$ if and only if it is equal to the intersection of a closed set of $X$ with $Y$.

Suppose that $A = C \cap Y$, where $C$ is closed in $X$. It follows that $X \backslash C$ is open, then by definition of the subspace topology, $(X \backslash C) \cap Y$ is open. Observe that $(X \backslash C) \cap Y = Y \backslash A$, so $Y \backslash A$ is open and thus $A$ is closed in $Y$ by definition.

Conversely, suppose that $A$ is closed in $Y$, then $Y \backslash A$ is open in $Y$, so by definition of subspace topology again it is equal to $Y \cap U$ where $U$ is open in $X$, which means that $X \backslash U$ is closed in $X$. Note that $A = Y \cap (X \backslash U)$, so $A$ is equal to the intersection of a closed set of $X$ with $Y$.

[Theorem 17.3] Let $Y$ be a subspace of $X$. If $A$ is closed in $Y$ and $Y$ is closed in $X$, then $A$ is closed in $X$.

A proof of this is a solution to Exercise 17.2.

Definition. Let $A$ be a subset of a topological space $X$. The interior of $A$, denoted by $\mathrm{int} A$, is defined as the union of all open sets contained in $A$. The closure of $A$, denoted by $\overline{A}$, is defined as the intersection of all closed sets containing $A$. In fact, we have the following relationship:

$$\mathrm{int} A \subseteq A \subseteq \overline{A}.$$

Another important fact is that $A$ is open if and only if $A=\mathrm{int} A$, whereas $A$ is closed if and only if $A=\overline{A}$.

tip

Informally, one can imagine that $\mathrm{int} A$ is constructed 'bottom-up from inside $A$' whereas $\overline{A}$ is constructed 'top-down from outside $A$'.

[Theorem 17.4] Let $Y$ be a subspace of $X$; let $A$ be a subset of $Y$; let $\overline{A}$ denote the closure of $A$ in $X$. Then the closure of $A$ in $Y$ equals $\overline{A} \cap Y$.

Let $B$ denote the closure of $A$ in $Y$. The set $\overline{A}$ is closed in $X$, so $\overline{A} \cap Y$ is closed in $Y$, by Theorem 17.2. Note as well that $\overline{A} \cap Y$ contains $A$, and by definition $B$ is the intersection of all closed subsets of $Y$ containing $A$, so we must have $B \subseteq (\overline{A} \cap Y)$.

Conversely, we know that $B$ is closed in $Y$, so by Theorem 17.2, $B = C \cap Y$ for some set $C$ closed in $X$. It follows that $C$ is a closed set of $X$ containing $A$. Since $\overline{A}$ is the intersection of all such closed sets, we conclude that $\overline{A} \subseteq C$. Therefore, $(\overline{A} \cap Y) \subseteq (C \cap Y)= B$.

[Theorem 17.5] Let $A$ be a subset of the topological space $X$.

a. Then $x \in \overline{A}$ if and only if every open set $U$ containing $x$ intersects $A$ (i.e. the intersection is non-empty).

b. Supposing the topology of $X$ is given by a basis, then $x \in \overline{A}$ if and only if every basis element $B$ containing $x$ intersects $A$.

For (a), it suffices to prove the equivalent statement below:

$$x \notin \overline{A} \iff \text{there exists an open set } U \text{ containing } x \text{ that does not intersect } A.$$

If $x$ is not in $\overline{A}$, then the set $U = X \backslash \overline{A}$ is an open set $U$ containing $x$ that does not intersect $A$, as desired. Conversely, if there exists an open set $U$ containing $x$ which does not intersect $A$, then $X \backslash U$ is a closed set containing $A$. By the definition of the closure $\overline{A}$, the set $X \backslash U$ must contain $\overline{A}$ since it is closed. Therefore, $x$ cannot be in $\overline{A}$.

As for (b), it immediately follows from (a) due to the facts that every basis element $B$ containing $x$ is an open set and that every open set $U$ containing $x$ contains a basis element that contains $x$.

Note: we say that $U$ is a neighbourhood of $x$ if(f) $U$ is an open set containing $x$.

Limit Point

Definition. Let $A$ be a subset of a topological space $X$ and $x$ be a point of $X$. We say that $x$ is a limit point (or 'cluster point', or 'accumulation point') of $A$ if every neighbourhood of $x$ intersects $A$ in some point other than $x$ itself. This can be rephrased as: if $x$ is a limit point, then $V(x) \cap (A \backslash \{x\}) \neq \emptyset$, where $V(x)$ denotes an (arbitrary) neighbourhood of $x$, or that $x$ belongs to the closure of $A \backslash \{x\}$.

note

If a topological space is endowed with a metric, then the neighbourhood notation can be written as $V_\delta(x)$, where $\delta>0$ is a (positive) real number, and the arbitrariness of a neighbourhood of $x$ is represented by the arbitrariness of the values of $\delta$.

This is in fact the definition often employed in a calculus or real analysis course.

[Theorem 17.6] Let $A$ be a subset of a topological space $X$, then the closure of $A$ is equal to the union of $A$ and all of its limit (accumulation) points, i.e. if we denote the set of all limit points of $A$ by $A'$, then $\overline{A} = A \cup A'$.

If $x$ is in $A'$, then every neighbourhood of $x$ intersects $A$ (in a point different from $x$). Thus, by Theorem 17.5, $x$ belongs to $\overline{A}$. Hence $A' \subseteq \overline{A}$. Since by definition $A \subseteq \overline{A}$, it follows that $A \cup A' \subseteq \overline{A}$.

To demonstrate the reverse inclusion, we let $x$ be a point of $\overline{A}$ and show that $x \in A \cup A'$. If $x$ happens to lie in $A$, then $x \in A \cup A'$. If $x$ does not lie in $A$, since $x \in \overline{A}$, every neighbourhood $U$ of $x$ intersects $A$ (Theorem 17.5); as $x \notin A$, the set $U$ must intersect $A$ in a point different from $x$, so $x \in A'$ and thus $x \in A \cup A'$, as desired.

An immediately corollary [Corollary 17.7] from here is that: a subset of a topological space is closed if and only if it contains all limit points. This follows from the fact that $A$ is closed if and only if $A=\overline{A}$.

Hausdorff space

Motivation

In an arbitrary topological space, a sequence $\langle x_n \rangle_{n \in \mathbb{N}}$ of points of the space $X$ converges to the point $x$ of $X$ if, corresponding to each neighbourhood $U$ of $x$, there exists a postive integer $N$ such that $x_n \in U$ for all $n \geqslant N$.

warning

Notice the lack of a metric and $\varepsilon>0$ in the definition of convergence of a sequence in an arbitrary topological space. This implies that unlike in $\mathbb{R}$ and $\mathbb{R}^2$, there may be multiple points of convergence for a single sequence.

In addition, for arbitrary topological spaces, a one-point set may not be closed, unlike the spaces $\mathbb{R}$ and $\mathbb{R}^2$. The one-point set $\{b\}$ is not closed in the three-point set $S = \{a,b,c\}$ equipped with the topology $\mathcal{S} = \{\emptyset, S, \{a,b\},\{b\},\{b,c\}\}$.

These relatively counterintuitive phenomena lead to the notion of Hausdorff spaces, as mathematicians seek to rule them out in the study of topology.

Main Notes

Definition. A topological space $X$ is called a Hausdorff space (or, 'is Hausdorff') if for each pair $x_1, x_2 \in X$ such that they are distinct points, i.e. $x_1 \neq x_2$, there exist neighbourhoods $U_1$ of $x_1$ and $U_2$ of $x_2$ such that they are disjoint.

[Theorem 17.8] Every finite point set in a Hausdorff space $X$ is closed.

As the closedness of a set is preserved under finite unions, it suffices to show that every one-point set $\{x_0\}$ is closed. If $x \in X$ and $x \neq x_0$, then $x$ and $x_0$ have disjoint neighbourhoods $U$ and $V$ by the definition of a Hausdorff space. Since $U$ does not intersect $\{x_0\}$, the point $x$ cannot belong to the closure of the set $\{x_0\}$. Since the choice of $x$ here is arbitrary, it follows that the closure of the set $\{x_0\}$ is $\{x_0\}$ itself, implying that it is closed.

note

The condition for finite point sets to be closed is in fact weaker than the Hausdorff condition. For example, $\mathbb{R}$ in the finite complement topology is not a Hausdorff space, but it is a space in which finite point sets are closed.

There is a name for the condition that the finite point sets be closed: the $T_1$ axiom. (The reason of this strange terminology will be explained in Chapter 4.)

(Note: $\mathbb{R}$ in the finite complement topology satisfying the $T_1$ axiom follows immediately from the definition of the topology itself.)

Why is $\mathbb{R}$ in the finite complement topology not a Hausdorff space?

Suppose that $x_1, x_2 \in \mathbb{R}$ where $x_1 \neq x_2$. Assume that there exists a neighbourhood $U$ of $x_1$ and $V$ of $x_2$ such that $U \cap V = \emptyset$. This implies that $\mathbb{R} \backslash (U \cap V) = (\mathbb{R} \backslash U) \cup (\mathbb{R} \backslash V) = \mathbb{R}$, which is impossible because both $\mathbb{R} \backslash U$ and $\mathbb{R} \backslash V$ are supposed to be finite by the definition of the finite complement topology.

[Theorem 17.9] Let $X$ be a space satisfying the $T_1$ axiom and $A$ be a subset of $X$, then the point $x$ is a limit point of $A$ if and only if every neighbourhood of $x$ contains infinitely many points of $A$.

If every neighbourhood of $x$ intersects $A$ in infinitely many points, it certainly intersects $A$ in some points other than $x$ itself, so $x$ is a limit point of $A$.

Conversely, suppose that $x$ is a limit point of $A$, and assume that some neighbourhood $U$ of $x$ intersects $A$ in only finitely many points, then $U$ also intersects $A \backslash \{x\}$ in finitely many points, say, $x_1,\ldots,x_m$. Since $\{x_1,\ldots,x_m\}$ is a finite point set, it is closed under the $T_1$ axiom, so $X \backslash \{x_1,\ldots,x_m\}$ is open. This means that

$$U \cap (X \backslash \{x_1,\ldots.x_m\})$$

is a neighbourhood of $x$ that does not intersect $A \backslash \{x\}$ at all, contradicting the assumption that $x$ is a limit point of $A$.

As remarked above, the Hausdorff axiom eliminates the possibility of a sequence in a topological space $X$ converging to more than one point in $X$.

[Theorem 17.10] If $X$ is a Hausdorff space, then a sequence of points of $X$ converges to at most one point of $X$.

Suppose that $x_n$ is a sequence of points of $X$ that converges to $x$, then there is a positve integer $N$ that depends on each neighbourhood $U$ of $x$ such that $x_n \in U$ whenever $n \geqslant N$. If $y \neq x$, let $U$ and $V$ be disjoint neighbourhoods of $x$ and $y$, respectively. Since $U$ contains $x_n$ for all but finitely many values of $n$, the set $V$ cannot. Therefore, $x_n$ cannot converge to $y$.

In view of Theorem 17.10, if the sequence $x_n$ of points of the Hausdorff space $X$ converges to the point $x$ of $X$, we can write $x_n \to x$, and say that $x$ is the limit of the sequence $x_n$.

[Theorem 17.11] Every simply ordered set is a Hausdorff space in the order topology. The product of two Hausdorff spaces is a Hausdorff space. A subspace of a Hausdorff space is a Hausdorff space.

The proofs of the following results are solutions to Exercises 17.10, 17.11 and 17.12 respectively.

Continuous Functions

Let us consider continuous functions beyond real and complex numbers, by generalising them in any topological space.

Definition. Let $X$ and $Y$ be topological spaces. A function $f : X \to Y$ is said to be continuous if for each open subset $V$ of $Y$, the set $f^{-1}(V)$ is an open subset of $X$.

Note that if $V$ does not intersect the image set $f(X)$ of $f$, then $f^{-1}(V)$ is empty.

note

This definition is in fact the Global Continuity Theorem, which is considered a consequence if the continuity of a function is defined using the notion of metric spaces (a.k.a. the '$\varepsilon$-$\delta$ definition').

In fact, in real-valued functions of a real variable, i.e. functions in the form of $f : \mathbb{R} \to \mathbb{R}$, the $\varepsilon$-$\delta$ definition and the definition above are equivalent. To prove that the open set definition implies the $\varepsilon$-$\delta$ definition, it suffices to show that for each open $\varepsilon$-neighbourhood $V$ of $f(x_0) \in \mathbb{R}$, one can always find a suitable $\delta$-neighbourhood $U$ of $x_0 \in \mathbb{R}$ such that $f(U) \subseteq V$. As for the converse, see Exercise 18.1.

Detailed proof that the open set definition implies the $\varepsilon$-$\delta$ definition.

Let $f : \mathbb{R} \to \mathbb{R}$ be a continuous function. For any $x_0$ in $\mathbb{R}^n$ and $\varepsilon > 0$, the interval $V=f(x_0)-\varepsilon, f(x_0)+\varepsilon$ is a neighbourhood of $f(x_0)$ in the codomain $\mathbb{R}$. Thus, $f^{-1}(V)$ is an open set in the domain $\mathbb{R}$. As $f^{-1}(V)$ contains the point $x_0$, it contains some basis element $(a,b)$ about $x_0$.

Choose $\delta$ to be the smaller of the two numbers $x_0-a$ and $b-x_0$, then if $|x-x_0|<\delta$, the point $x$ must be in $(a,b)$, so that $f(x) \in V$, and thus $|f(x)-f(x_0)|< \varepsilon$, as desired.

note

The arguments above can be modified to prove the same for real multivariate functions, though this may require the notion of box topology or (general) product topology to define the standard topology on $\mathbb{R}^n$. Nevertheless, it is shown that the topology on $\mathbb{R}^n$ generated by (open) hyperrectangles and $n$-balls are the same.

However, this $\varepsilon$-$\delta$ definition, as well as the notion of sequential continuity do not generalise to arbitrary topological spaces, but they serve important roles in the study of metric spaces.

If the topology of the range space (codomain) $Y$ is generated by a basis $\mathcal{B}$, then to prove continuity it suffices to check that the inverse image of each basis element is open. Why?

Any open set $V$ of $Y$ can be written as a union of basis elements, i.e.

$$V = \bigcup_{\alpha \in J}B_\alpha.$$

Thus, since inverse images preserve unions, we have

$$f^{-1}(V) = \bigcup_{\alpha \in J}f^{-1}(B_\alpha).$$

We can then see that $f^{-1}(V)$ is open if each set $f^{-1}(B_\alpha)$ is open.

note

The same applies for a subbasis, as an arbitrary basis element $B$ for $Y$ can be expressed as a finite intersection $S_1 \cap \cdots \cap S_n$ of subbasis elements. Since $f^{-1}(B) = \bigcap_{i=1}^{n}f^{-1}(S_i)$, the inverse image of every basis element is open if the subbasis element is open.

[Theorem 18.1] Let $X$ and $Y$ be topological spaces; let $f : X \to Y$, then the following are equivalent:

1. $f$ is continuous.
2. For every subset $A$ of $X$, we have $f(\overline{A}) \subseteq \overline{f(A)}$.
3. For every closed set $B$ of $Y$, the set $f^{-1}(B)$ is closed in $X$.
4. For each $x \in X$ and each neighbourhood $V$ of $f(x)$, there is a neighbourhood $U$ of $x$ such that $f(U) \subseteq V$.

If the condition 4. holds for the point $x$ of $X$, we say that $f$ is continuous at the point $x$.

(1) $\implies$ (2). Assume that $f$ is continuous. Let $A$ be a subset of $X$. We show that if $x \in \overline{A}$, then $f(x) \in \overline{f(A)}$. Since $f$ is continuous, if $V$ is a neighbourhood of $f(x)$, then $f^{-1}(V)$ is an open set of $X$ containing $x$, so it must intersect $A$ in some point $y$ by Theorem 17.5. It follows that $V$ intersects $f(A)$ in the point $f(y)$, so that $f(x) \in \overline{f(A)}$ as desired.

Homeomorphisms

Definition. Let $X$ and $Y$ be topological spaces and $f : X \to Y$ be a bijection. If both the function $f$ and the inverse function $f^{-1} : Y \to X$ are continuous, then $f$ is called a homeomorphism.

info

Note that the continuity of the (bijective) inverse function $f^{-1}$ requires its inverse image of an open set $U$ of $X$ to be open, which is the same as saying the image of an open set $U$ of $X$ under $f$ is open.

This gives rise to an equivalent formulation of homeomorphisms, which is that $f : X \to Y$ is a homeomorphism if and only if $f$ is a continuous bijection and for any open set $U$ of $X$, the image $f(U)$ is also open in $Y$.

Homeomorphisms are remarkable in the sense that they act like isomorphisms in abstract algebra: they give bijective correspondences between the collections of open sets that preserve the topological structure between two spaces, as well as topological properties (i.e. properties that are entirely expressed in terms of open sets).

If $f : X \to Y$ is an injective continuous map, $Z$ is the image set $f(X)$, considered as a subspace of $Y$, and $f' : X \to Z$ is a homeomorphism, we say that $f : X \to Y$ is a (topological) imbedding (or 'embedding') of $X$ in $Y$.

[Theorem 18.2] (Rules for constructing continuous functions). Let $X$, $Y$ and $Z$ be topological spaces.

1. (Constant function) If $f : X \to Y$ maps all of $X$ into the single point $y_0$ of $Y$, then $f$ is continuous.
2. (Inclusion) If $A$ is a subspace of $X$, the inclusion function $j : A \to X$ is continuous.
3. (Composites) If $f : X \to Y$ and $g : Y \to Z$ are continuous, then the map $g \circ f : X \to Z$ is continuous.
4. (Domain restriction) If $f : X \to Y$ is continuous, and if $A$ is a subspace of $X$, then the restricted function $f|_A : A \to Y$ is continuous.
5. (Range restriction or expansion) Let $f : X \to Y$ be continuous. If $Z$ is a subspace of $Y$ containing the image set $f(X)$, then the function $g : X \to Z$ obtained by restricting the range of $f$ is continuous. If $Z$ is a space with $Y$ being a subspace, then the function $h : X \to Z$ obtained by expanding the range of $f$ is continuous.
6. (Local formulation of continuity) If $X$ can be written as the union of open sets $U_\alpha$ such that $f|_{U_\alpha}$ is continuous for each $\alpha$, then the map $f : X \to Y$ is continuous.

note

In analysis, taking sums, difference, products or quotients of continuous real-valued functions yields us a continuous function as well. This can be generalised to functions with domains being an arbitrary topological space $X$, but the range still being $\mathbb{R}$.

[Theorem 18.3] (Pasting Lemma). Let $X = A \cup B$, where $A$ and $B$ are both closed in $X$. Let $f : A \to Y$ and $g : B \to Y$ be continuous. If $f(x)=g(x)$ for every $x \in A \cap B$, then $f$ and $g$ combine to give a continuous function $h : X \to Y$, defined by $h(x)=\begin{cases} f(x) & \text{if } x \in A, \\ g(x) & \text{if } x \in B \end{cases}$.

(Note that the requirement that $f(x)=g(x)$ for every $x \in A \cap B$ is so that $h : X \to Y$ is well-defined as a function.)

If $A$ and $B$ are closed in $X$, consider a closed subset of $Y$, denoted here by $C$. Note that

$$h^{-1}(C) = f^{-1}(C) \cup g^{-1}(C).$$

Since $f$ is continuous, $f^{-1}(C)$ is closed in $A$ (by Theorem 18.1), and thus closed in $X$. Similarly, $g^{-1}(C)$ is closed in $B$ and hence closed in $X$. Their (finite) union $h^{-1}(C)$ is thus closed in $X$, so $h$ is continuous.

note

If $A$ and $B$ are open in $X$, it immediately follows from the 'local formulation of continuity' rule in Theorem 18.2.

[Theorem 18.4] (Maps into products). Let $f : A \to X \times Y$ be given by the equation $f(a)=(f_1(a), f_2(a))$, then $f$ is continuous if and only if the functions $f_1 : A \to X$ and $f_2 : A \to Y$ are continuous.

(The maps $f_1$ and $f_2$ are called the coordinate functions of $f$.)

note

There is no useful criterion for the continuity of maps like $f : A \times B \to X$ with the product space being the domain, one might guess that $f$ is continuous if it is continuous 'in each variable separately,' but this conjecture is not true. See Exercise 12 for a counterexample proof.

Footnotes

1. A generalisation of the subspace topology (as well as product topology) is the initial topology, which confusingly is also called the induced topology. Hence, the name 'induced topology' will hereon be avoided so that ambiguity does not arise. ↩