Chapter 2: Topological Spaces and Continuous Functions

Topology and Topological Spaces: A Primer

The study of topological spaces is a generalisation of the concepts of metric spaces, as well as open and closed sets, both of which are important in real analysis. Informally, a topological space is a set that has a topology, which "decides" which subset is open or not.

Definition. A topology $\mathcal{T}$ on a set $X$ is a collection of subsets of $X$ (in other words, $\mathcal{T} \subseteq \mathcal{P}(X)$) which has the following properties:

1. The empty set $\emptyset$ and $X$ itself are in $\mathcal{T}$.
2. Any arbitrary union of subcollections of $\mathcal{T}$ is in $\mathcal{T}$.
3. Any finite intersection of subcollections of $\mathcal{T}$ is in $\mathcal{T}$.

We can then say that a subset $U$ of $X$ is an open set if $X$ is in $\mathcal{T}$. One can compare this with the metric-space definition of open sets, which is the definition often adapted in real analysis courses and can allow us to derive the topological definition of open sets in $X$, as described above.

One may then ask: what if it is the other way round, i.e. is it possible to produce a metric space from a topological space? In fact, this is a question that attracts so much interest that mathematicians assign a special name to those that have this property: metrizable spaces, which we shall learn later in this chapter.

This may look obvious to some, but for the sake of reminder: it is possible for a set $X$ to have multiple topologies. There is also a not-so-obvious one: different sets can have the same topology(!).

Concepts for Topologies

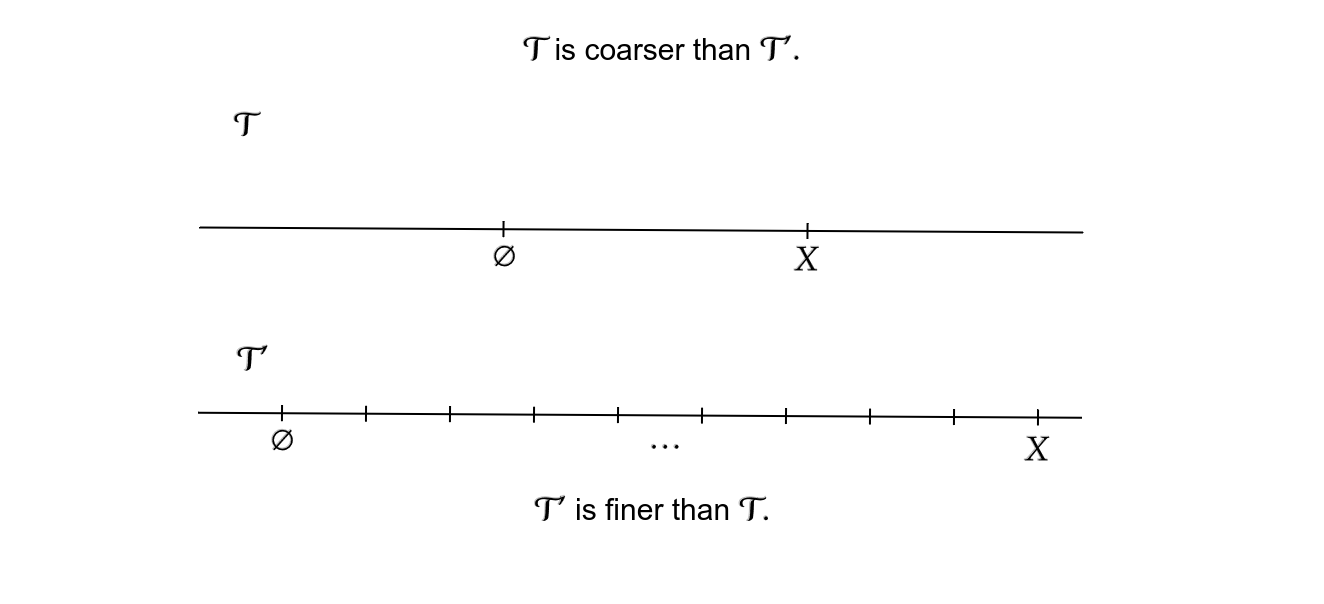
Fineness and Coarseness

Definition. Given (any) two topologies $\mathcal{T}, \mathcal{T'}$ of a set $X$, we say that $\mathcal{T'}$ is finer than $\mathcal{T}$ if $\boxed{\mathcal{T'} \supseteq \mathcal{T}}$. We say $\mathcal{T'}$ is strictly finer than $\mathcal{T}$ if $\boxed{\mathcal{T'} \supset \mathcal{T}}$.

Conversely, if $\boxed{\mathcal{T'} \subseteq \mathcal{T}}$ (resp. $\boxed{\mathcal{T'} \subset \mathcal{T}}$), then we say that $\mathcal{T'}$ is coarser (resp. strictly coarser) than $\mathcal{T}$.

We say $\mathcal{T}$ and $\mathcal{T'}$ are comparable if either $\mathcal{T'} \supseteq \mathcal{T}$ or $\mathcal{T'} \subseteq \mathcal{T}$, i.e. if it is possible to say if one is finer or coarser than the other.

Informally, a topology is finer if it "contains more detail" or "has a finer scale" than the other topology.

A visualisation of topological coarseness and fineness using ruler markings.

Basis (for a Topology)

Definition. Let $X$ be a set. A basis for a topology $\mathcal{T}$ on $X$ is a collection of subsets of $X$ (which are called basis elements), denoted here as $\mathcal{B}$, such that for each $x \in X$:-

1. There is at least one basis element $B$ that contains $x$, i.e. $x \in B$.
2. If $x \in B_1 \cap B_2$, where $B_1$ and $B_2$ are (two) basis elements, then there is a (third) basis element $B_3$ such that $x \in B_3$ and $B_3$ is contained by the intersection of $B_1$ and $B_2$, i.e. $B_3 \subseteq B_1 \cap B_2$. (Note: this is immediately true if $B_1 = B_2$: the desired $B_3$ will just be $B_1 = B_2$ itself.)

The topology $\mathcal{T}$ generated by the basis $\mathcal{B}$ is then defined as: if a subset $U$ of $X$ is open (i.e. $U \in \mathcal{T}$), then for each $x \in U$, there is a basis element $B \in \mathcal{B}$ such that $x \in B$ and $B \subseteq U$. From the definition, we can see that the basis elements themselves are in the topology generated from them.

Why does this definition of basis-generated topology do give us a topology?

We need to check that a topology $\mathcal{T}$ generated by a basis $\mathcal{B}$ satisfies the basic definition of topology.

If $U = \emptyset$, then $U \in \mathcal{T}$ vacuously because we cannot find any $x \in U$ to check the condition of openness. If $U = X$, then since every basis element $B \in \mathcal{B}$ satisfies $B \subseteq X$, as well as the first condition for a basis, it also satisfies this condition of openness and is thus in $\mathcal{T}$.

To check that any arbitrary union of $\mathcal{T}$, i.e. $U = \bigcup_{\alpha \in J}U_\alpha$, where $\{U_\alpha\}_{\alpha \in J}$ is an indexed family of sets in $\mathcal{T}$, is still in $\mathcal{T}$, we see that since each $U_\alpha$ is open, by definition, there is a basis element $B$ such that $x \in B \subseteq U_\alpha$. Note that $U_\alpha \subseteq U$ for any $\alpha \in J$, so we have $B \subseteq U$ as well. This shows that $U$ is open and hence in $\mathcal{T}$.

To check that any finite intersection of $\mathcal{T}$, i.e. $U = \bigcap_{i=1}^{n}U_i$, where $U_1,\ldots, U_n \in \mathcal{T}$ and $n \in \mathbb{N}$, is in $\mathcal{T}$, we can do so by induction. We first settle the base case: for $n = 1$, $U_1$ itself is already in $\mathcal{T}$, so it immediately holds.

When $n = 2$ so that we have $U_1 \cap U_2$, given $x \in U_1 \cap U_2$, by definition, we can choose basis elements $B_1$ and $B_2$ such that $x \in B_1$ (resp. $B_2$) and $B_1 \subseteq U_1$ (resp. $B_2 \subseteq U_2$). By the definition of a basis, we can obtain a basis element $B_3$ such that $x \in B_3$ and $B_3 \subseteq B_1 \cap B_2$. Since $B_1 \cap B_2 \subseteq U_1 \cap U_2$, this gives us $B_3 \subseteq U_1 \cap U_2$, so $U_1 \cap U_2 \in \mathcal{T}$, by definition.

This argument above can be used to prove the inductive case. For a finite intersection $U_1 \cap \cdots \cap U_n$ of elements of $\mathcal{T}$, we first suppose that $U_1 \cap \cdots \cap U_{n-1}$ does belong to $\mathcal{T}$. Now, note that

$$(U_1 \cap \cdots \cap U_n) = (U_1 \cap \cdots \cap U_{n-1}) \cap U_n.$$

Therefore, by induction hypothesis and applying the argument above, we can conclude that any finite intersection of elements in $\mathcal{T}$ belongs to $\mathcal{T}$.

We have then checked that all three conditions of a topology are satisifed, so $\mathcal{T}$ indeed gives us a topology.

If $X$ is any set, the collection of all one-point subsets (singletons) of $X$ is a basis for the discrete topology on $X$. Why?

Let $X$ be a set and $\mathcal{B}$ be the collection of all one-point subsets of $X$. Since there is a one-to-one correspondence, specifically $x \mapsto \{x\}$, between $X$ and $\mathcal{B}$, this allows us to conclude that for any $x \in X$, there exists at least one basis element $B \in \mathcal{B}$ such that $x \in B$, giving us the first condition for a basis. Due to this one-to-one correspondence as well, there is no elements in $X$ that belongs to two different basis elements, so the second condition for a basis holds vacuously.

Any arbitrary union of the one-point subsets $B \in \mathcal{B}$ will give us $\mathcal{P}(X) \backslash \{\emptyset\}$, i.e. the collection of all subsets of $X$ except for the empty set, and this indeed includes $X$ itself. Any finite intersection of $B$ will then give us the last piece of the puzzle: the empty set $\emptyset$.

This finally gives us the complete $\mathcal{P}(X)$, i.e. the discrete topology on $X$.

[Lemma 13.1] $\mathcal{T}$ as a topology on a set $X$ that is generated by a basis $\mathcal{B}$ can also be described as the collection of all unions of elements of $\mathcal{B}$.

Why?

For any given collection of elements of $\mathcal{B}$, since they are also elements of $\mathcal{T}$ and $\mathcal{T}$ is a topology, their union is also in $\mathcal{T}$.

Conversely, for any $U \in \mathcal{T}$, we can find for each $x \in U$ a basis element $B_x \in \mathcal{B}$ such that $x \in B_x \subseteq U$, so $U = \bigcup_{x \in U}B_x$, and thus $U$ equals a union of elements of $\mathcal{B}$.

This means that any open set $U$ in $X$ can be expressed a union of basis elements, which sounds analogous to bases in linear algebra in which vectors are expressed as a linear combination of basis vectors. However, such expression needs not be unique, which makes it different from bases in linear algebra.

In reverse, we can also obtain a basis for a given topology, which is a frequently cited fact in the study of this topic.

[Lemma 13.2] Let $X$ be a topological space. Suppose that $\mathcal{C}$ is a collection of open sets of $X$ such that for each open set $U$ of $X$ and each $x$ in $U$, there is an element $C$ of $\mathcal{C}$ such that $x \in C \subseteq U$, then $\mathcal{C}$ is a basis for the topology of $X$. Why?

We need to check that $\mathcal{C}$ satisifies the defining conditions of a (topological) basis. Since $X$ is a topological space and thus is an open set itself, by the hypothesis for $\mathcal{C}$, for each $x \in U$, there is an element $C$ of $\mathcal{C}$ such that $x \in C \subseteq X$, so the first condition is satisfied.

To check the second condition, suppose that $x \in C_1 \cap C_2$, where $C_1,C_2 \in \mathcal{C}$. Since $C_1$ and $C_2$ are open, so is $C_1 \cap C_2$. Therefore, there exists by hypothesis an element $C_3$ in $\mathcal{C}$ such that $x \in C_3 \subseteq C_1 \cap C_2$.

Let $\mathcal{T}$ be the collection of open sets of $X$; we also need to show that the topology $\mathcal{T}'$ generated by $\mathcal{C}$ is indeed equal to the topology $\mathcal{T}$. First, note that if $U$ belongs to $\mathcal{T}$ and if $x \in U$, then there is by hypothesis an element C of $\mathcal{C}$ such that $x \in C \subseteq U$, so $U$ belongs to the (generated) topology $\mathcal{T}'$. Conversely, if $W$ belongs to the (generated) topology $\mathcal{T}'$, then $W$ equals a union of elements of $\mathcal{C}$, by Lemma 13.1. Since each element of $\mathcal{C}$ belongs to $\mathcal{T}$ and $\mathcal{T}$ is a topology, $W$ also belongs to $\mathcal{T}$.

[Lemma 13.3] Let $\mathcal{B}$ and $\mathcal{B}'$ be bases for the topologies $\mathcal{T}$ and $\mathcal{T}'$, respectively, on $X$, then $\mathcal{T}'$ is finer than $\mathcal{T}$ if and only if for each $x \in X$ and each basis element $B \in \mathcal{B}$ containing $x$, there is a basis element $B' \in \mathcal{B}'$ such that $x \in B' \subseteq B$.

Proof of Lemma 13.3.

$(\impliedby)$. Given an element $U$ of $\mathcal{T}$, we wish to show that $U \in \mathcal{T}'$. Let $x \in U$. Since $\mathcal{B}$ generates $\mathcal{T}$, there is an element $B \in \mathcal{B}$ such that $x \in B \subseteq U$. By hypothesis, there exists an element $B' \in \mathcal{B}'$ such that $x \in B' \subseteq B$, then $x \in B' \subseteq U$, so $U \in \mathcal{T}$ by definition.

$(\implies)$. Let $x \in X$ and $B \in \mathcal{B}$, with $x \in B$. Now $B$ belongs to $\mathcal{T}$ by definition and $\mathcal{T} \subseteq \mathcal{T}'$ by hypothesis (being finer). Therefore, $B \in \mathcal{T}'$. Since $\mathcal{T}'$ is generated by $\mathcal{B}'$, there is an element such that $x \in B' \subseteq B$.

Lemma 13.3 also shows that the collection of all circular regions in the plane generates the same topology as the collection of all rectangular regions.

Important Topologies

There are several main topologies covered in this chapter. Some of them are so important that they deserve a dedicated subsection, whereas some others that are not so much are just included as an item of a bullet list here. Here, we denote a set as $X$, and its equipped topology, unless otherwise stated, as $\mathcal{T}$.

• Discrete topology: the collection of all subsets of $X$.
• Indiscrete/trivial topology: the other end of the extreme, i.e. the collection of only $\emptyset$ and $X$ itself.
• Finite complement topology, $\mathcal{T}_f$: the collection of all subsets $U$ of $X$ such that $X \backslash U$ is either finite or $X$ itself (so that $U = \emptyset$).
• Countable complement topology, $\mathcal{T}_c$: the collection of all subsets $U$ of $X$ such that $X \backslash U$ is either countable or $X$ itself (so that $U = \emptyset$).
• Standard topology (on the real line), $\mathbb{R}$: the topology generated by the collection of all open intervals in the real line, $(a,b)=\{x : a < x < b\}$. This is assumed to be the default topology for $\mathbb{R}$, unless otherwise stated.
• Lower limit topology, $\mathbb{R}_l$: the topology generated by the collection of all half-open intervals of the form $[a,b) = \{x : a \leqslant x < b\}$, where $a < b$.
• K-topology, $\mathbb{R}_K$: the topology generated by the collection of all open intervals $(a,b)$, along with all sets of the form $(a,b) \backslash K$, where $K = \left\{\frac{1}{n} : n \in \mathbb{Z}_+ \right\}$.

Order Topology

Product Topology (+ Box Topology)

Subspace Topology

Metric Topology

Quotient Topology